Introduction:

In this quick tutorial, we’ll first start by looking at the brute-force solution to find the middle element in the linked list. Later, we’ll learn how to achieve it in a single iteration through the entire linked list i.e. in just a single pass.

Problem Definition:

Given a linked list L, our aim is to design an algorithm to find the middle element of this linked list. If the size of the given linked list is even, then it has two middle elements. For such a case, our solution should return the second element among the two.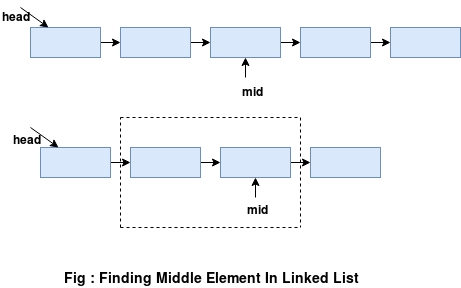

Brute-Force Solution:

It’s pretty intuitive that if we know the size of the linked list, we can easily return the middle element. This solution, therefore, involves below simple steps:

1. Finding the size, say n, of the linked list by counting the number of nodes in it
2. Again traversing the linked list till we reach n/2th element in the list
3. Return n/2th element as the output

Let’s write some code:

public Node findMiddleElementBruteForce(Node head) {
    int n = size(head);
    for(int i = 0; i < n/2; i++) {
        head = head.next;
    }
    return head;
}

public int size(Node head) {
    Node tmp = head;
    int count = 0;
    while(head != null) {
        count++;
        head = head.next;
    }
    return count;
}

Here, head refers to the first node of our linked list. Also, it’s important for us to note that this solution traverses the linked list twice and so isn’t very efficient.

Hare-And-Tortoise Approach(Single Pass):

As the name suggests, the central idea behind this approach involves using two pointers – fastPtr and slowPtr. Here, our fastPtr moves twice as fast as the slowPtr. So by the time our fastPtr reaches the end of the linked list, our slowPtr will be pointing to the middle element.

Let’s implement this solution:

public Node findMiddleElement(Node head) {
    Node fastPtr = head, slowPtr = head;
    while(fastPtr != null && fastPtr.next != null) {
        slowPtr = slowPtr.next;
        fastPtr = fastPtr.next.next;
    }
    return slowPtr;
}

When using the above approach, we’re able to find the middle element of a linked list in a single iteration. We would strongly recommend you to draw it out on a paper to grasp a deeper understanding on how it works.

Conclusion:

In this tutorial, we learned to solve a famous programming interview question on linked lists i.e. how to find the middle element for a given linked list. We covered the brute-force approach followed by a more efficient way involving the use of two pointers.